EJERCICIOS

1. RESUELVE


Hasta este momento la proporción áurea parece haberse considerado una propiedad geométrica y no hay ningún signo obvio de que se intentase asociar un número con la relación. Por supuesto, si AB tiene longitud 1 y AC = x, donde C divide AB en la proporción áurea, entonces podemos usar álgebra sencilla para hallar x.

1/x = x/ (1-x) da x^2 + X - 1 = 0 por lo tanto x = (√5 - 1)/2. Entonces la relación áurea es 1/x = (√5 + 1)/2 = 1.6180339887498948482...

2. CONSTRUYE UN RECTÁNGULO ÁUREO

La proporciÓn áurea o divina, fue descubierta por los griegos y relaciona los lados de un rectángulo llamado precisamente áureo o divino.

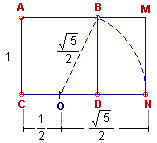
Para que un rectángulo sea áureo, debe cumplirse que a: b=(a+b): a igual a una constante llamada sección áurea y cuyo valor es (1+x5)/2 cuyo valor aproximado es 1,6180339...
Muchas construcciones griegas antiguas como el Partenón en Atenas y también otras modernas en todo el mundo han sido construidas usando estas proporciones, por el particular sentido de armonía que generan los rectángulos construidos de esta manera.

1. Tu primera misión es calcular las dimensiones que debe tener una caja rectangular cuyo lado menor esta dado y vale 20 cm, para que esten lo más aproximadamente posible en sección áurea.

2. Tu segunda misión es medir objetos rectangulares (cajas de zapatos, interruptores de luz, marcos de puertas y ventanas, etc.), anotar cuidadosamente sus medidas y comprobar si están o no en proporción aurea. Verifica, además, si aquellos que están aproximadamente en proporción áurea se ven más armoniosos o no.

3. CALCULA

Aplicando la proporción áurea obtenemos la siguiente ecuación que tendremos que resolver

Una de las soluciones de esta ecuación (la solución positiva) es x=

Lo sorprendente ahora es calcular el valor que se obtiene al dividir el segmento mayor entre el menor

Es decir, la relación entre las dos partes en que dividimos el segmento es el número de oro.